从1加到99等于多少

从1加到99的和是一个等差数列求和的问题，这个和可以通过公式计算得出。等差数列求和公式是：(首项 + 末项) * 项数 / 2。在这个例子中，首项是1，末项是99，项数是99（因为是从1加到99）。所以，和S为：

\[ S = \frac{1 + 99}{2} \times 99 = \frac{100}{2} \times 99 = 50 \times 99 \]

\[ S = 4950 \]

从1加到99的和是4950。

对于求从1加到99的平方，这个并不是一个简单加法，因为每个数都是它自己的平方。从1到99的数列中，每个数乘以它自己会得到一个平方数序列，其和可以用不同的方法来求，比如矩形数（1^2 + 2^2 + ... + n^2）的和公式是 (n(n + 1)(2n + 1)) / 6。但对于99的平方，我们可以直接计算：

\[ 99^2 = 9801 \]

所以，从1加到99的平方是9801。

从1加到99等于多少简便运算

从1加到99的和可以通过简便方法计算。这是一个常见的等差数列求和问题，其中首项a1 = 1，末项an = 99，项数n = 99。等差数列求和公式为：

\[ S_n = \frac{n(a_1 + a_n)}{2} \]

代入数值得到：

\[ S_{99} = \frac{99(1 + 99)}{2} \]
\[ S_{99} = \frac{99 \times 100}{2} \]
\[ S_{99} = 99 \times 50 \]
\[ S_{99} = 4950 \]

所以，从1加到99的和是4950，这是一个简便快捷的方法。

从1加到99等于多少怎么算法

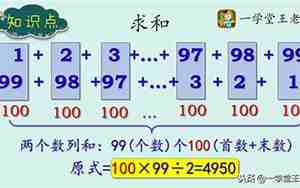
从1加到99的和可以通过配对求和的方式来简便计算。这个方法基于这样的观察：每一对相邻的数，它们的和是100（比如1+99，2+98，...，49+51），共有49对这样的数。

所以，总和可以看作是49个100相加，再加上中间的一个数50（因为1和99、2和98、...，一共99个数，正好是49对加1个50）。

计算如下：

\[ S = 49 \times 100 + 50 = 4900 + 50 = 4950 \]

所以，从1加到99等于4950。这是求和的一种简单算法。

从1加到99等于多少简便方法

从1加到99的简便计算方法是利用高斯求和公式，也叫做等差数列求和。因为这个数列是连续的自然数，它们的和可以看做是前50个自然数之和（从1到50）再加50（50 + 51 + ... + 99 = 49*50 + 50）。

具体步骤如下：

1. 前50个自然数之和是 \((1 + 99) \times 50 / 2\)，这是一个等差数列的和，等于\(50 \times 50\).
2. 加上50（50+51+...+99）。

所以，\(S = (1 + 99) \times 50 / 2 + 50 = 100 \times 50 / 2 + 50 = 5000 + 50 = 4950\)。

因此，从1加到99等于4950，这是个简便且直观的计算方法。