圆柱的表面积的公式

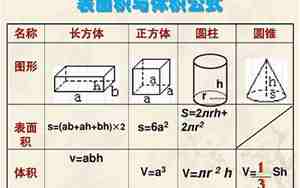
圆柱的表面积公式分为两个部分：侧面积和底面积的和。

1. 侧面积（侧柱面）：对于一个圆柱，侧面积是底面圆周长乘以高。圆柱的底面半径为 \( r \)，高为 \( h \)，侧面积 \( S_{侧} \) 计算如下：
\[ S_{侧} = 2\pi rh \]

2. 底面积：圆柱有两个底面，每个底面都是圆，面积为圆周率乘以半径的平方：
\[ S_{底} = 2\pi r^2 \]

圆柱的表面积 \( S_{总} \) 就是侧面积和两个底面积之和：
\[ S_{总} = S_{侧} + 2S_{底} = 2\pi rh + 2\pi r^2 \]

所以，圆柱的表面积公式可以写作：
\[ S_{总} = 2\pi r(h + r) \]

这个公式中，\( r \) 是圆柱底面的半径，\( h \) 是圆柱的高度。如果需要计算具体的表面积，只需代入相应的数值即可。

圆柱的表面积的公式用字母怎么写

圆柱的表面积公式用字母表示如下：

设圆柱的底面半径为 \( r \)，高为 \( h \)，则其表面积 \( S_{总} \) 用字母表示为：

\[ S_{总} = 2\pi r(h + r) \]

其中，\( \pi \) 是圆周率，大约等于 3.14159。这个公式可以用于计算任意圆柱的表面积。只需要将半径 \( r \) 和高 \( h \) 替换为具体的数值即可。

圆柱的表面积的公式推导过程

圆柱的表面积的公式推导过程基于圆柱的基本形状和几何性质。圆柱由两个圆面（底面）和一个长方形（侧面）组成。

1. 底面积（两个底面）：
每个底面都是一个圆，半径为 \( r \)。圆面积的公式是 \( A = \pi r^2 \)。因为有两个底面，所以底面积总和为：
\[ 2A_{底} = 2\pi r^2 \]

2. 侧面积（侧面）：
侧面是圆柱的侧面展开图，形状是长方形，长是圆周长 \( 2\pi r \)，宽是高 \( h \)。侧面积 \( A_{侧} \) 就是长乘以宽：
\[ A_{侧} = 2\pi r \cdot h \]

3. 表面积总和：
圆柱的表面积是底面积和侧面积之和：
\[ S_{总} = A_{底} + A_{侧} = 2\pi r^2 + 2\pi rh \]
\[ S_{总} = 2\pi r(r + h) \]

这样就得到了圆柱的表面积公式。这个公式是基于圆柱的基本结构和几何形状来推导的。