液体的沸点和大气压有什么关系

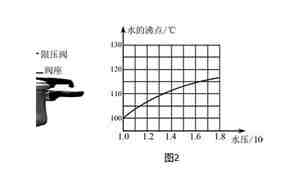
液体的沸点是指液体在标准大气压下变为气态的温度。当大气压强发生变化时，液体的沸点也会相应地发生调整。沸点与大气压的关系遵循著名的"盖-吕萨克定律"和"查理定律"，在理想气体模型中，它表述为：

1. 盖-吕萨克定律：对于一定量的气体，如果温度保持不变，那么气体的体积与压力成反比。当大气压降低时，液体上方的气体压力减小，液面上的蒸汽压也会降低，使得液体需要更高的温度才能沸腾，即沸点上升。

2. 查理定律：对于理想气体，无论体积如何，其压强与绝对温度成正比。同样，如果降低大气压，液体的沸点会随着气压的减小而降低，因为沸点是液体分子克服表面张力转变为气态的临界点，气压减小意味着分子克服阻力的阈值更低。

总结来说，液体的沸点与大气压直接相关：在标准大气压下，沸点是固定的；若气压降低，沸点会上升；若气压升高，沸点则会降低。这是因为在较低的气压下，液体分子需要更多的能量才能达到沸点，反之亦然。

液体沸点与大气压的关系公式

液体的沸点确实与大气压有关，这是由于沸点反映了液体分子从液态变为气态的临界能量。其关系可以通过克劳修斯-克拉珀龙方程来表示，这是一个理想气体状态方程的推广形式，适用于液体的蒸气压和沸点：

\[ P = \frac{RT}{v_m - b} \]

在这个公式中：
\( P \) 是气压（包括液体上方的蒸气压），
\( R \) 是气体常数，
\( T \) 是绝对温度（以开尔文为单位），
\( v_m \) 是液体的摩尔体积（在沸点时液体和蒸汽的平均体积），
\( b \) 是液体的饱和蒸气压项（也称为范德华常数，反映了分子间相互作用的影响）。

对于纯液体，当\( T \)等于沸点时，\( v_m \)会显著变大，因为液态转变为气态，而\( b \)是一个固定值。所以，沸点\( T_b \)可以表达为：

\[ P_b = \frac{R T_b}{v_m(T_b) - b} \]

这里，\( P_b \) 是沸点时的气压。通过解这个方程，我们可以估算不同大气压下液体的沸点。实际应用中，大气压的标准值（1大气压，即101，325帕斯卡）通常用来计算沸点，除非特别指定其他气压条件。